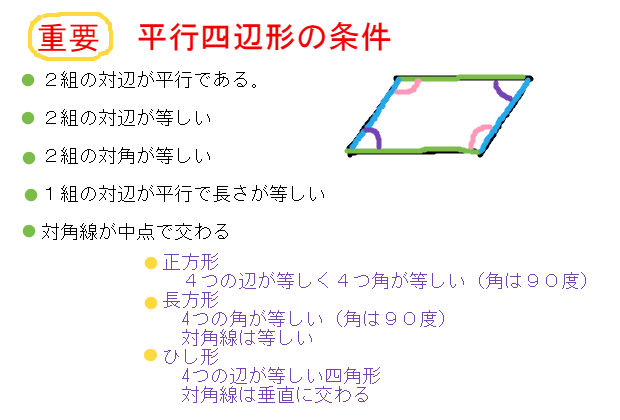
平行四辺形の性質と条件 4章 平行と合同(中2学年) 5 多角形の内角と外角 拡大、縮小 対頂角、平行線の性質と条件 相似な図形、相 図形の性質の調べ方 三角形の合同条件 平行線と線分の比 証明のしくみ 中点連結定理 5章 平面図形(中1学年)三角形の合同の証明の利用 四角形 \(abcd\) が平行四辺形であることを示すために、 辺の長さ、角の大きさが等しいことを示したいときがあります。 これを示すために、 「三角形の合同を証明し、そこから示す」 ということ平行四辺形の合同条件 ①2組の対辺はそれぞれ平行である ②2組の対辺はそれぞれ等しい ③2組の対角はそれぞれ等しい ④対角線はそれぞれの中点で交わる ⑤1組の対辺は、平行で長さが等しい この回答
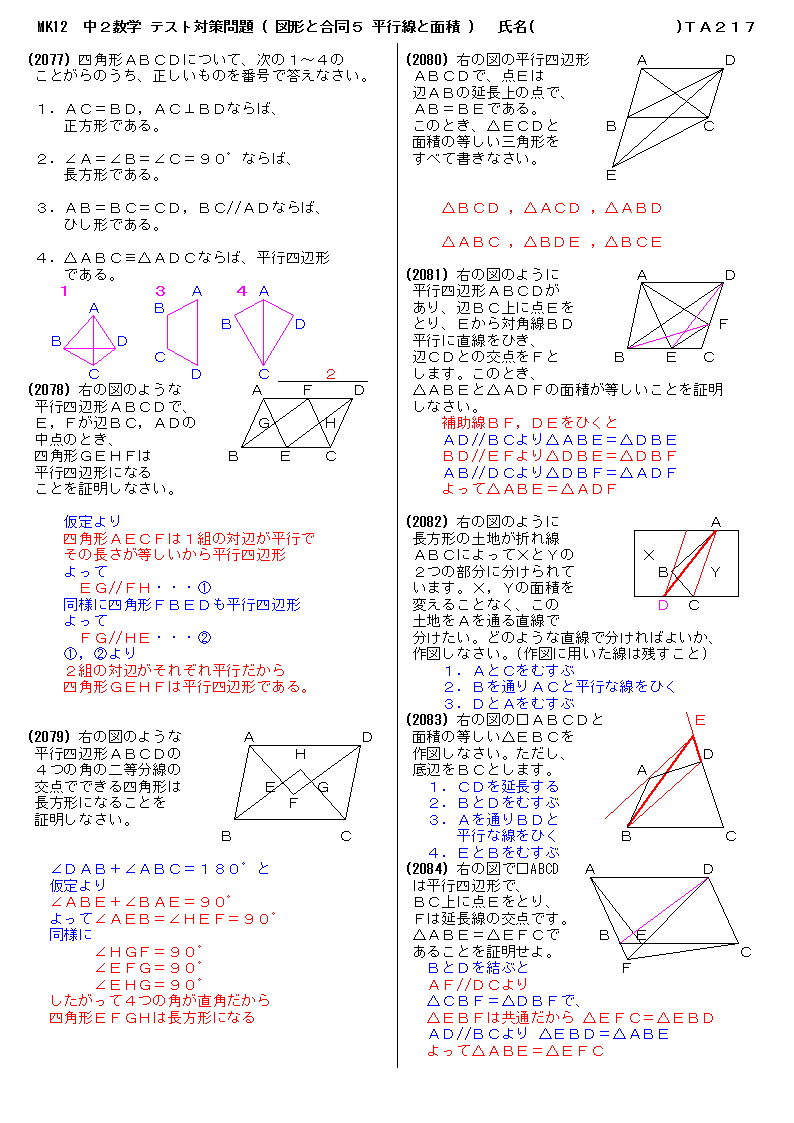
無料 中2数学 テスト対策 解答プリント 217 図形と合同5 平行線と面積
平行四辺形 合同 証明
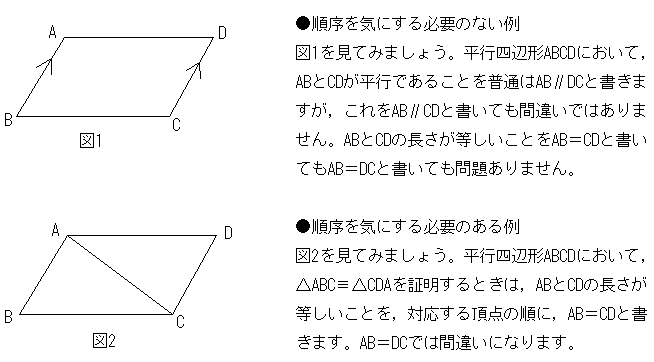
平行四辺形 合同 証明-定義は「こういう四角形を平行四辺形としよう」と決めたことなので、これを証明することはできません。 「なぜ平行四辺形の向かい合う2組の辺は平行なのか?」と問われたら、 「そのような四角形が平行四辺形と定義されているから」 という答えになってしまいます。1 合同と証明 11 合同な図形 ある図形を他の図形にぴったり重ね合わすことができるとき、2 つの図形は合同であるといいます。図形を ぴったり重ねるには、 ⃝1 平行移動(ずらす) ⃝2 回転移動(回す) ⃝3 対称移動(裏返す)




ม 2 โน ตของ 中2数学 平行四辺形の証明 授業ノート ช น Clear
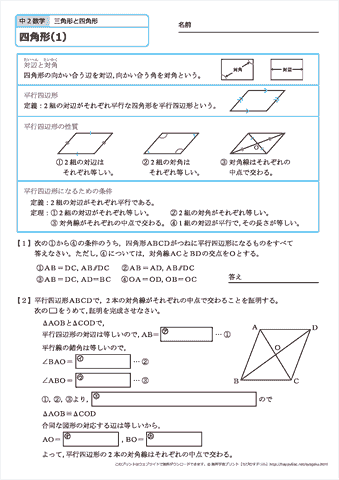
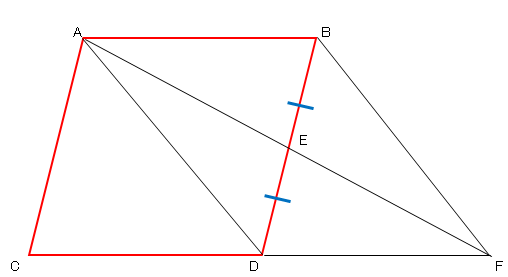
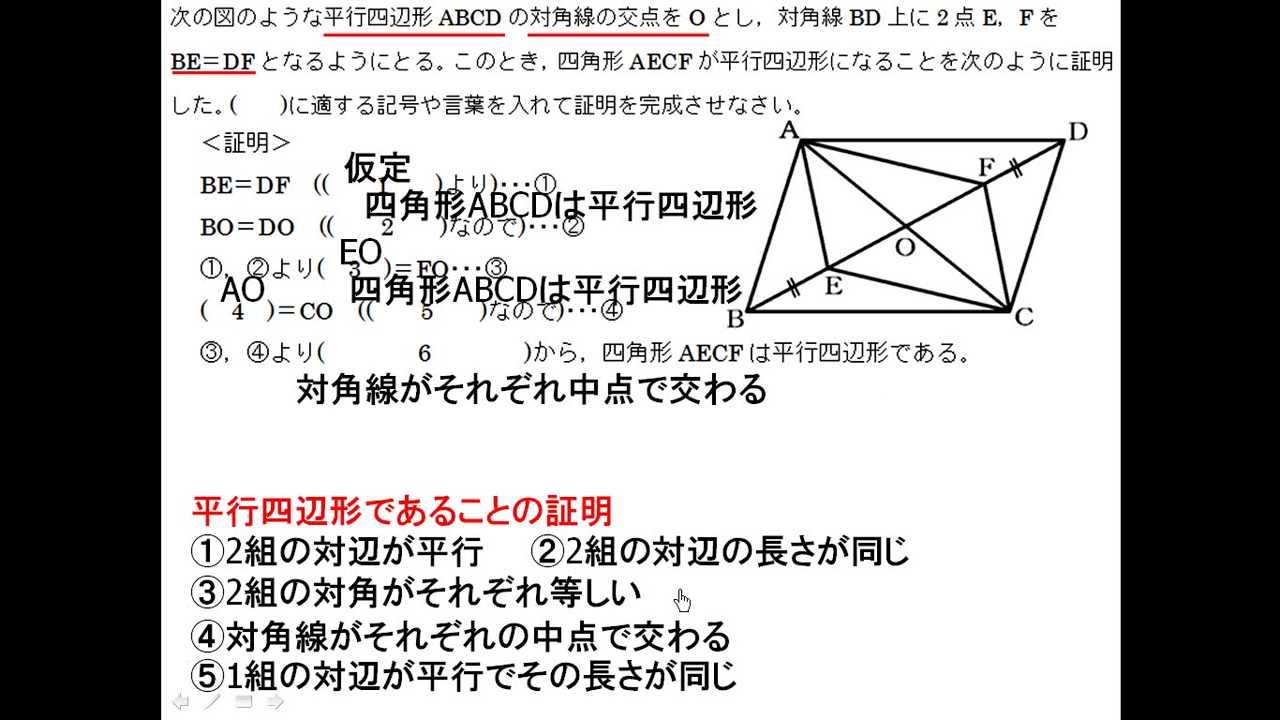
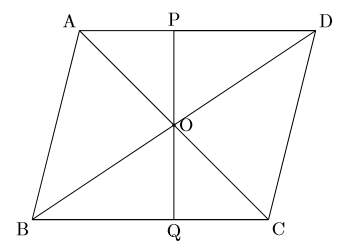
平行と合同 例題 平行線の錯角・同位角 補助線を引く問題 三角形の内角と外角の関係 印をつけた角の和 角の二等分線と内角の和 三角形の合同証明1 三角形の合同証明2(辺の共通) 三角形の合同証明3(角の平行四辺形の証明2 名前 平行四辺形abcdのad,dmの中点を それぞれm,nとするとき、bm=dnであることを 証明しなさい。 平行四辺形の対角線の交点oを通る直線をひき ac,bdの交点をp,qとする。このとき op=pqであることを証明しなさい。 平行四辺形abcdの∠aの二等分線平行四辺形 ⇒ ( ならば) 1組が平行でかつ等しい も当然〇となりますね! では本題、その逆は? ⑤'四角形abcdの1組の対辺が平行でかつ等しい ⇒ ( ならば) 平行四辺形? (証明) 対角線ac、bdを引く oadと ocbにおいて ad//bcより ∠oad = ∠ocb (錯角) ①
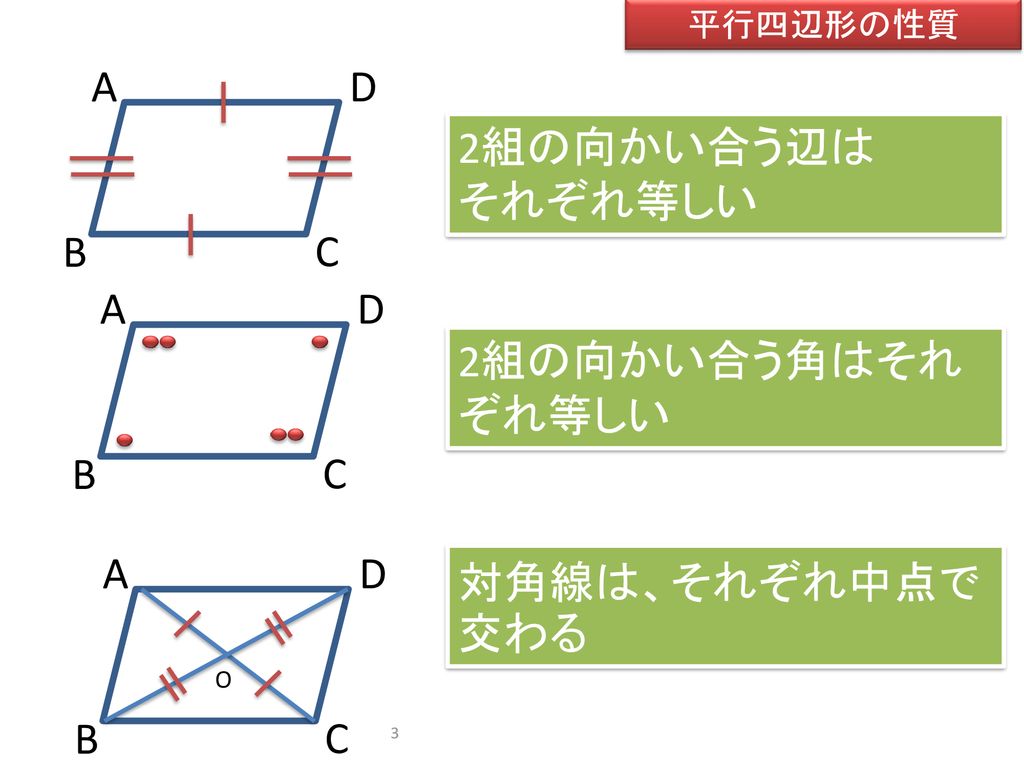
平行四辺形の定義 2組の対辺がそれぞれ 平行な四角形 性質1 2組の対辺は それぞれ等しい 性質2 2組の対角は それぞれ等しい 性質3 対角線はそれぞれの 中点で交わる。 そのためには、 図形の証明で使う最低限の知識(図形の性質、合同条件等)を頭に叩き込んで下さい。大した量ではありません。その後、「証明の書き方」を覚えます。 テンプレート化しちゃうんです。 あとは基本の証明問題を10問練習し模試レベルに移行。証明しなさい。 ③ 平行四辺形の対角線は, それぞれの中点で交わる。 ② 平行四辺形の向かいあう角は等しい。 ① 平行四辺形の向かい合う辺は等しい。 平行四辺形の性質 2組の向かいあう辺が, それぞれ平行な四辺形を平行四辺形という。 §1 平行四辺形
平行四辺形になるための条件 四角形 \(abcd\) が平行四辺形であることを示せ。 このような問題を学習していきます。 四角形 \(abcd\) が平行四辺形であることを示すためには、 以下の \(5\) つのうち、ど合同な図形 三角形の合同条件を 用いて,2つの三角 形が合同であるかど うかを考えることが できる。 平行線と角 「三角形の内角の和 は180°である」こ となどを,平行線の 性質を用いて説明す ることができる。 平行四辺形 図形の性質を証明す合同 ・図形の証明をよみ,そこから新たな性質を 見いだすことができる。 ・2つの直角三角形の合同を,直角三角形の 合同条件を用いて判断することができる。 ・直角三角形の合同条件を理解している。 課題プリント 定期テスト 8 9 10 平行四辺形の 性質




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット




平行四辺形であることを証明する 苦手な数学を簡単に
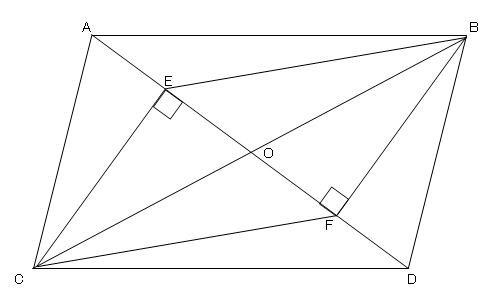
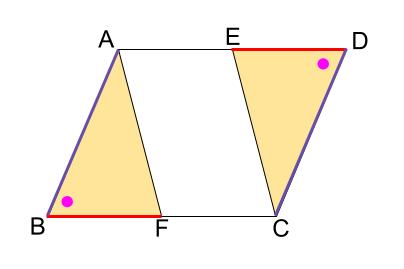
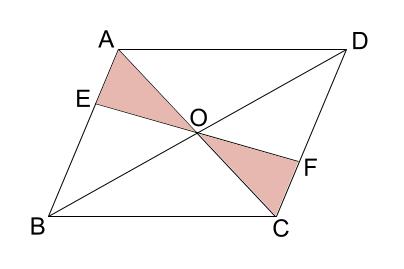
平行四辺形の性質を利用した証明 平行四辺形の内外にある三角形の合同を証明する問題もあるよ。三角形の合同条件を改めて確認しておこう。 (1)3辺がそれぞれ等しい。 (2)2辺とその間の角がそれ角, 円, 外接円, 合同, 作図, 幾何, 中線, 平行四辺形, ひし形, 回転, 正方形, 三角形 中学生でも解ける、大学生でも解けない難問。 ジオジェブラの作図機能を使って考えてみよう。 ジオジェブラは正確なので、図に頼らないで、なぜそのことが言えるのかを平行四辺形の性質を利用した証明 次の証明をしなさい。 合同な三角形の対応する辺は等しいので ae=cf aeo と cfo において ao=co (平行四辺形の対角線はそれぞれの中点で交わる) ∠aoe=∠cof (対頂角) ∠eao=∠fco (ab//cd 錯角)



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




平行四辺形になることの証明 Youtube
仮定と結論,逆,合同条件/三角形の合同の証明/二等辺三角形の定理/ 二等辺三角形の性質を使った証明 /二等辺三角形になることを証明/正三角形/ 直角三角形/ 平行四辺形の性質/平行四辺形になるための条件/長方形・ひし形・正方形/ 折り返し3-6.平面図形 合同の証明 複合問題ほか 09年度出題 問1 図において,線分ab上に点d,線分ac上に点eがあり,線分cdと線分beの交点をfとする。ad=ae, ∠adc=∠aebであるとき, acdと合同な三角形を答えなさい。中2数学。2つの「辺の長さ」が等しいことを証明せよ。ヤバいこれも合同証明? それとも違うの? 図形はムズカシイ(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 証明問題はコツがある!(ビシッ)無料サイトだ。



平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download



平行四辺形の合同の証明問題と角度を求める問題 数学の要点まとめ 練習問題一覧
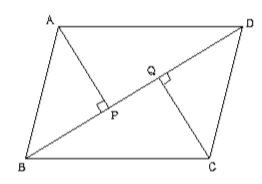
平行四辺形の定義は、「\(\boldsymbol{2}\) 組の向かい合う辺が平行な四角形を平行四辺形という 」になります。また、平行四辺形になるためには、定義を含めて \(\boldsymbol{5}\) つの条件 があります。平行四辺形の証明1 名前 右の四角形abcdが平行四辺形であるとき、 向かい合う2組の辺が等しいことを証明しなさい。 平行四辺形の対角線bdに垂線ae,cf ひくと、ae=cfとなることを証明しなさい。 平行四辺形abcdの辺bcの中点をmとし、aとmを結ぶ合同証明応用(直線と内角の和) 合同証明応用(角の引き算) 二等辺三角形の角 平行四辺形証明 折り返し 平行線と面積 等積変形1 等積変形2 三角形・四角形 練習問題
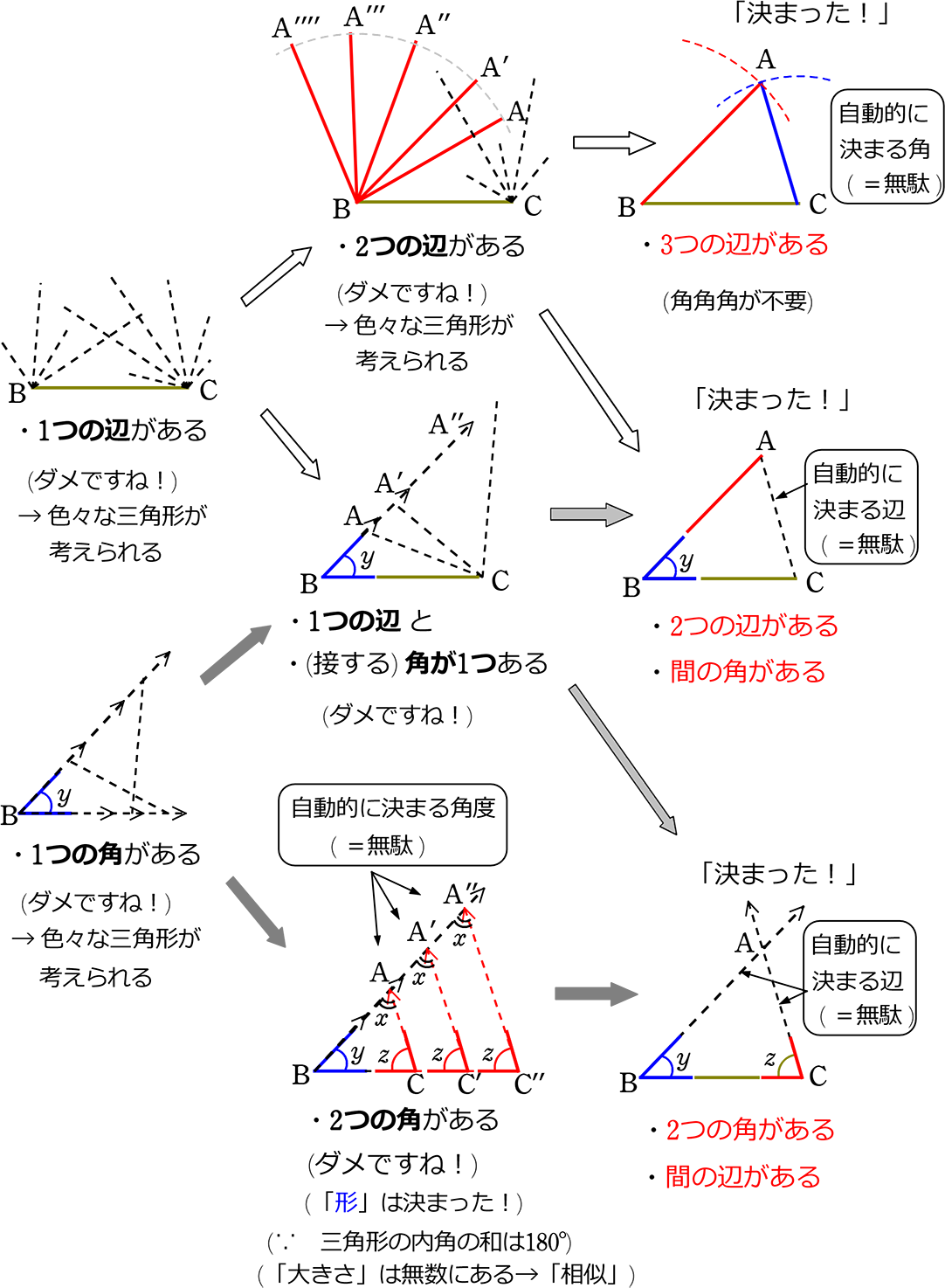



中学数学 図形の合同 図形の性質



平行四辺形の性質を使った証明 平行四辺形になることの証明 チーム エン
命題の逆を示し、証明する。 3 直角三角形の合同(2) 直角三角形の合同条件を用いて、図形の性質を証明する。 4 平行四辺形の性質(3) 平行四辺形の性質などを証明する。 5 平行四辺形になるための条件(3) 平行四辺形になるための条件を証明する。AE=CFとなることが証明できました! 三角形の合同条件や平行四辺形になるための 条件を用いて,AE=CFとなることを証明 してみましょう。 桃子さんの証明を振り返ってみましょう。 桃子さんは何に着目して証明していますか。平行四辺形とひし形の違いってなに?? 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説!←今回の記事 等積変形三角形の面積問題と作図のやり方は?証明問題も紹介!




中2数学 三角形と四角形 章の問題a 赤城 ᐡᐤᐡ
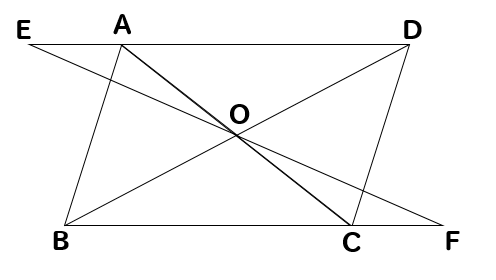



中学数学 平行四辺形の証明問題を徹底解説 数スタ
⑤ 直角三角形の合同条件を証明する。 ⑥ 直角三角形の合同条件を使って,いろいろな図形を証明する。 ⑦・⑧ 平行四辺形の定義を知り,その性質を証明する。 ⑨ 四角形が平行四辺形になる条件を考え,それらを証明する。 展開例 シミュレーション教材平行四辺形の特徴を、証明の手がかりにする んだ。 POINT 「証明の記述は得意じゃないな~」という人は、4章「図形の性質と合同」で学習した 「ハンバーガーの3ステップ」 を意識して、証明の文章を書くことを思い出してね。 Step2 平行四辺形の性質をつかう! 長方形は平行四辺形の1種だったね?? ってことは、 平行四辺形の性質がつかえるってわけ。 よって、 2組のむかいあう辺がそれぞれ等しい より、 AB = DC ・・・(2) になるね。 Step3 三角形の合同条件をつかう! BCは




無料 中2数学 テスト対策 解答プリント 217 図形と合同5 平行線と面積
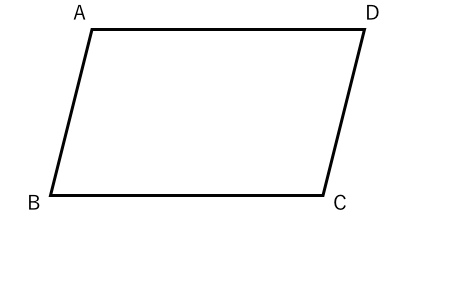



合同な三角形 平行四辺形で証明 苦手な数学を簡単に
二等辺三角形 z 二等辺三角形の性質 z 二等辺三角形であるための条件 z 正三角形 z 直角三角形の合同 z 直角三角形の合同条件を使った証明 z 平行四辺形 z 平行四辺形の性質 z 平行四辺形であるための条件 z いろいろな平行四辺形 z 平行線と面積 z 円周角2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。(定義) 2 2組の向かいあう辺が、それぞれ等しい。(証明) 3 2組の向かいあう角が、それぞれ等しい。(証明)




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




数学 中2 74 平行四辺形になる条件 Youtube
平行四辺形になる条件 2組の向かいあう辺が、ぞれぞれ平行であるとき(定義) 2組の向かいあう辺が、それぞれ等しいと 「平行四辺形の性質」 平行四辺形に対角線を一本引いたときにできる三角形の合同を証明しようと すると、すべての合同条件を用いて




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学



数学の証明の問題です 平行四辺形abcdの外側に 辺ab をそれ Yahoo 知恵袋
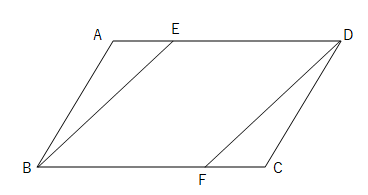



中2数学 平行四辺形の証明のポイントと練習問題 Examee




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
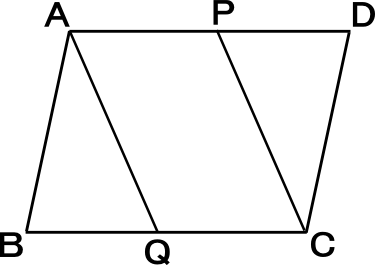



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学




Math 平行四辺形 平行四辺形になることの証明 働きアリ
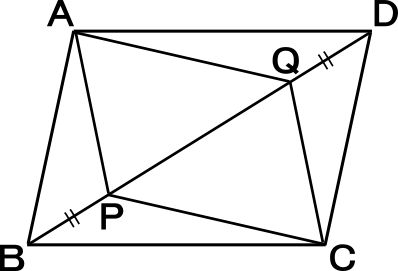



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同
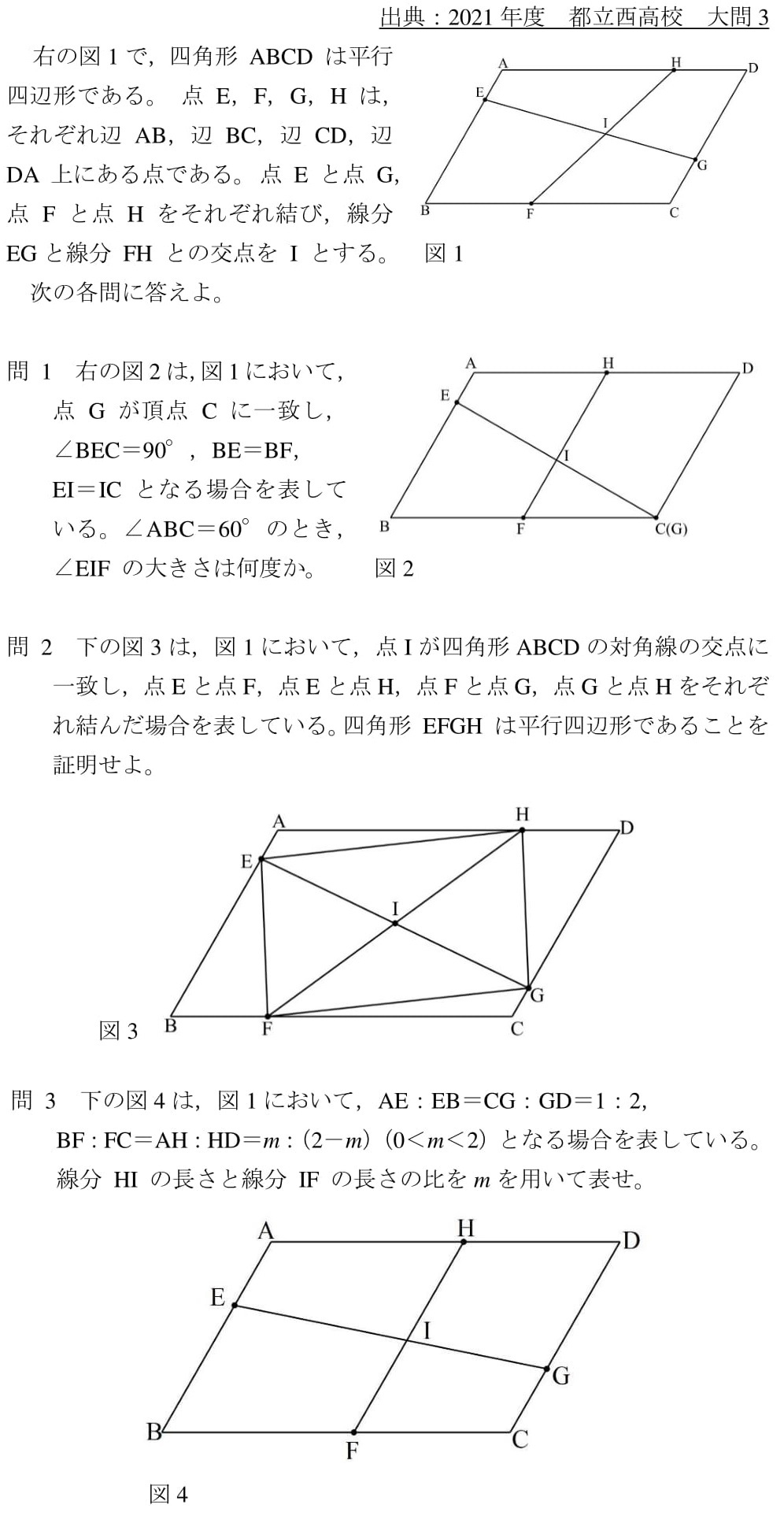



21都立西 平行四辺形の難問証明 高校入試 数学 良問 難問
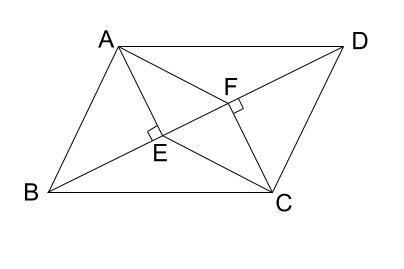



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル
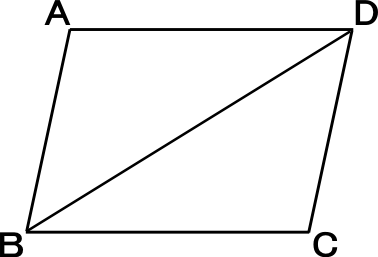



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同
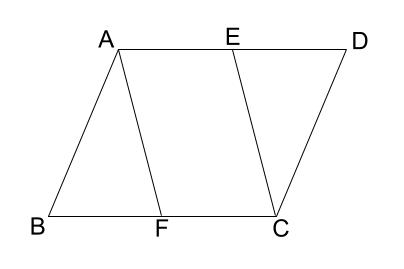



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
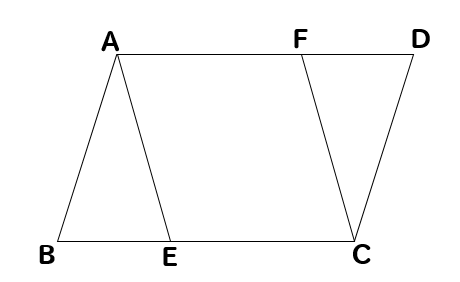



中学数学 平行四辺形の証明問題を徹底解説 数スタ



1
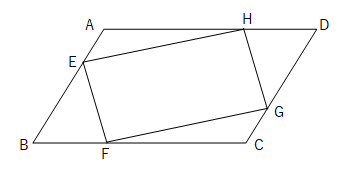



中2数学 平行四辺形の証明のポイントと練習問題 Examee



合同な三角形 平行四辺形で証明 苦手な数学を簡単に



高校入試 英語 数学 学習 三角形と四角形 平行四辺形




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




平行四辺形を使った証明 Youtube




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット
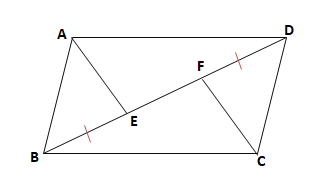



中2数学 平行四辺形の性質と証明の要点まとめノート 中学生勉強サイトあかね先生
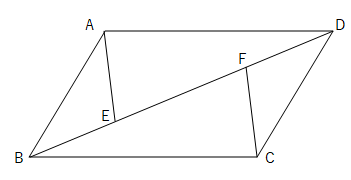



中2数学 平行四辺形の証明の定期テスト予想問題 Pikuu



平行四辺形になるための証明3



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




平行四辺形の証明問題 無料で使える中学学習プリント




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




平行四辺形の性質 と ひし形の性質 を比べる とちぎeライブラリ
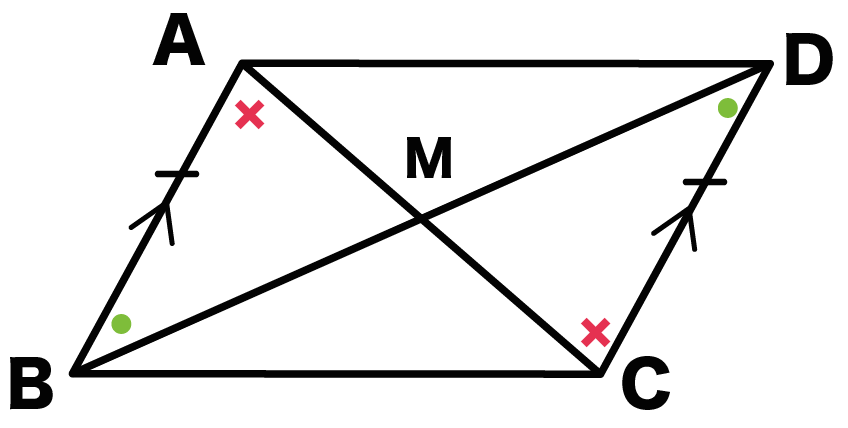



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
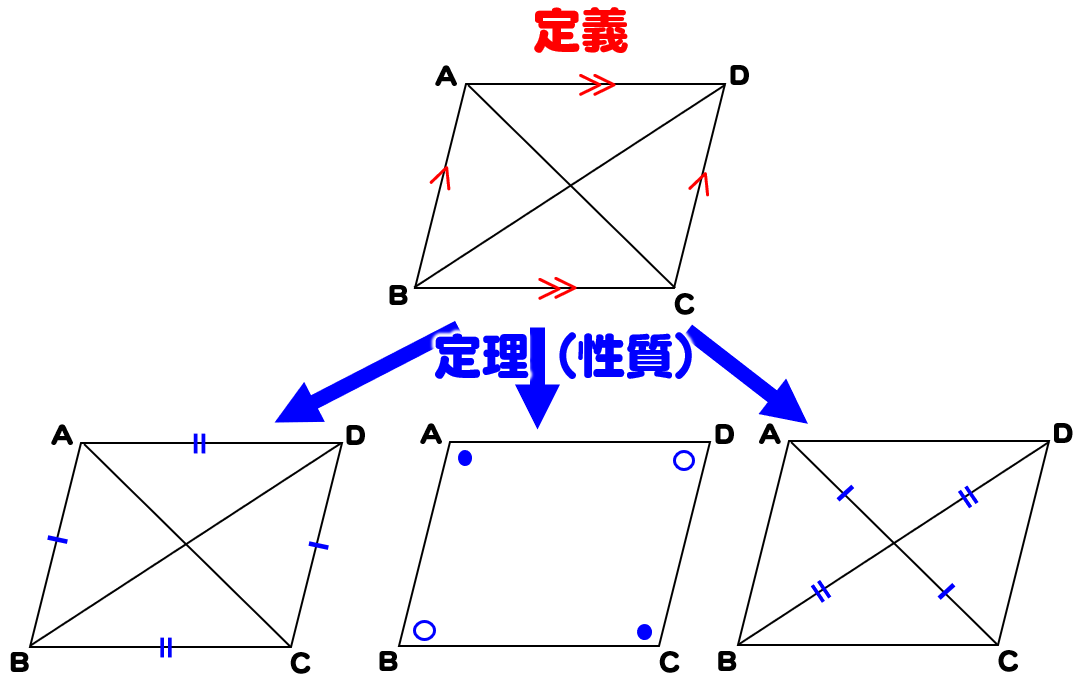



平行四辺形の定義と性質 証明問題の解き方 数学fun




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
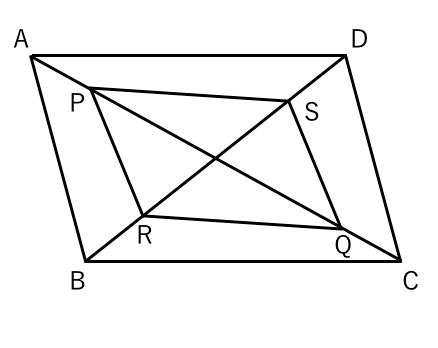



平行四辺形であることを証明する 苦手な数学を簡単に
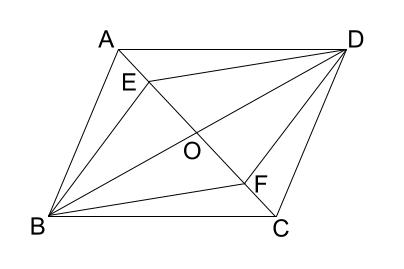



中学数学 平行四辺形になることの証明 その1 中学数学の無料オンライン学習サイトchu Su
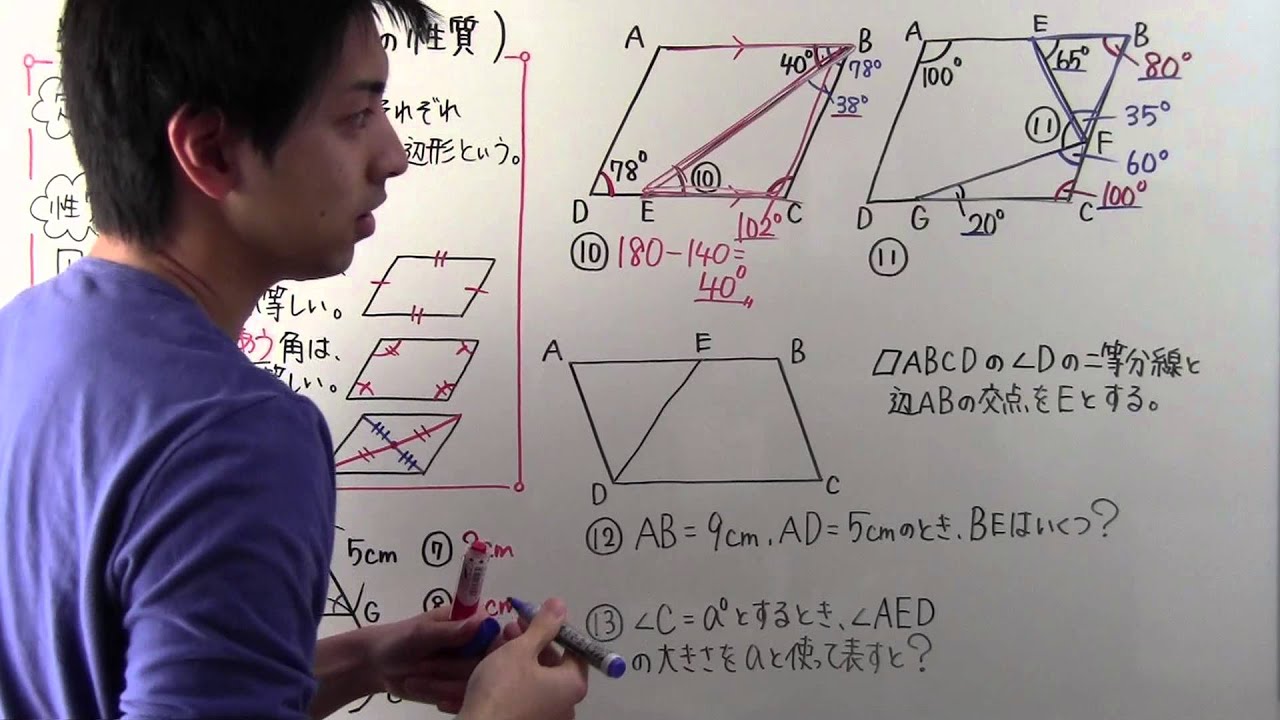



数学 中2 73 平行四辺形の性質 Youtube




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方
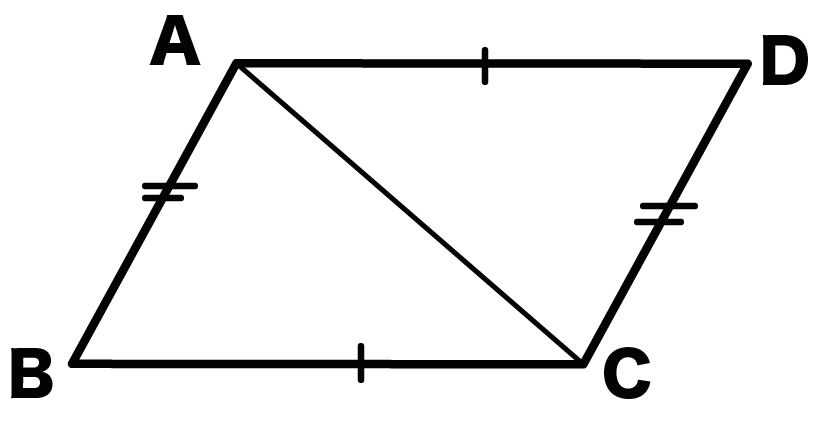



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
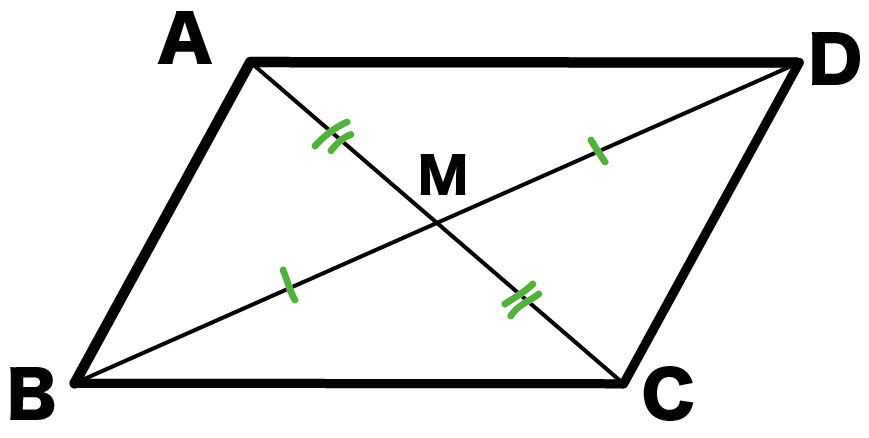



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく



平行四辺形の性質の利用2



平行四辺形になるための証明3
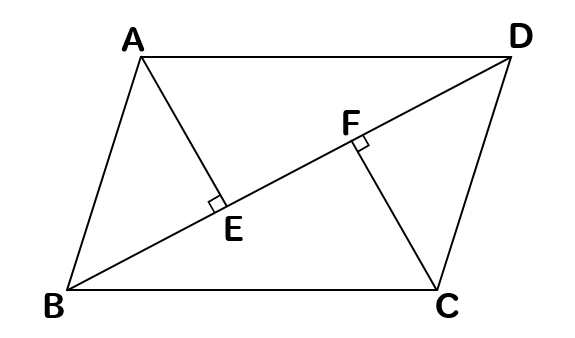



中学数学 平行四辺形の証明問題を徹底解説 数スタ




平行四辺形になるための条件 Youtube




誰かー 平行四辺形の合同条件を使った証明の問題 ムズいやつ出してくれませんか Clear



三角形の合同の応用問題 制限3分 中学数学 理科 寺子屋塾の復習サイト



平行四辺形の証明 4 ネット塾




Abeと Cdfが合同ということを証明 Ebcと Fdaが合同ということを証明 Clear



中2数学 基本問題プリント12 平行四辺形1 性質 問題 230




中学数学 平行四辺形の証明問題を徹底解説 数スタ




平行四辺形の証明問題 無料で使える中学学習プリント



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



至急 数学証明平行四辺形の折り目の問題です どなたかご教示お願い致し Yahoo 知恵袋




中学数学 平行四辺形の証明問題を徹底解説 数スタ



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




3 Abcd Ac Ab Cf Aecf Descubre Como Resolverlo En Qanda



平行四辺形の証明 2 ネット塾




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
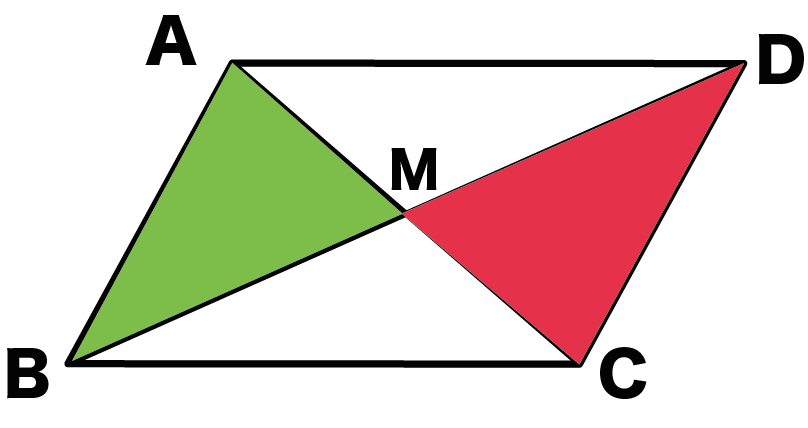



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
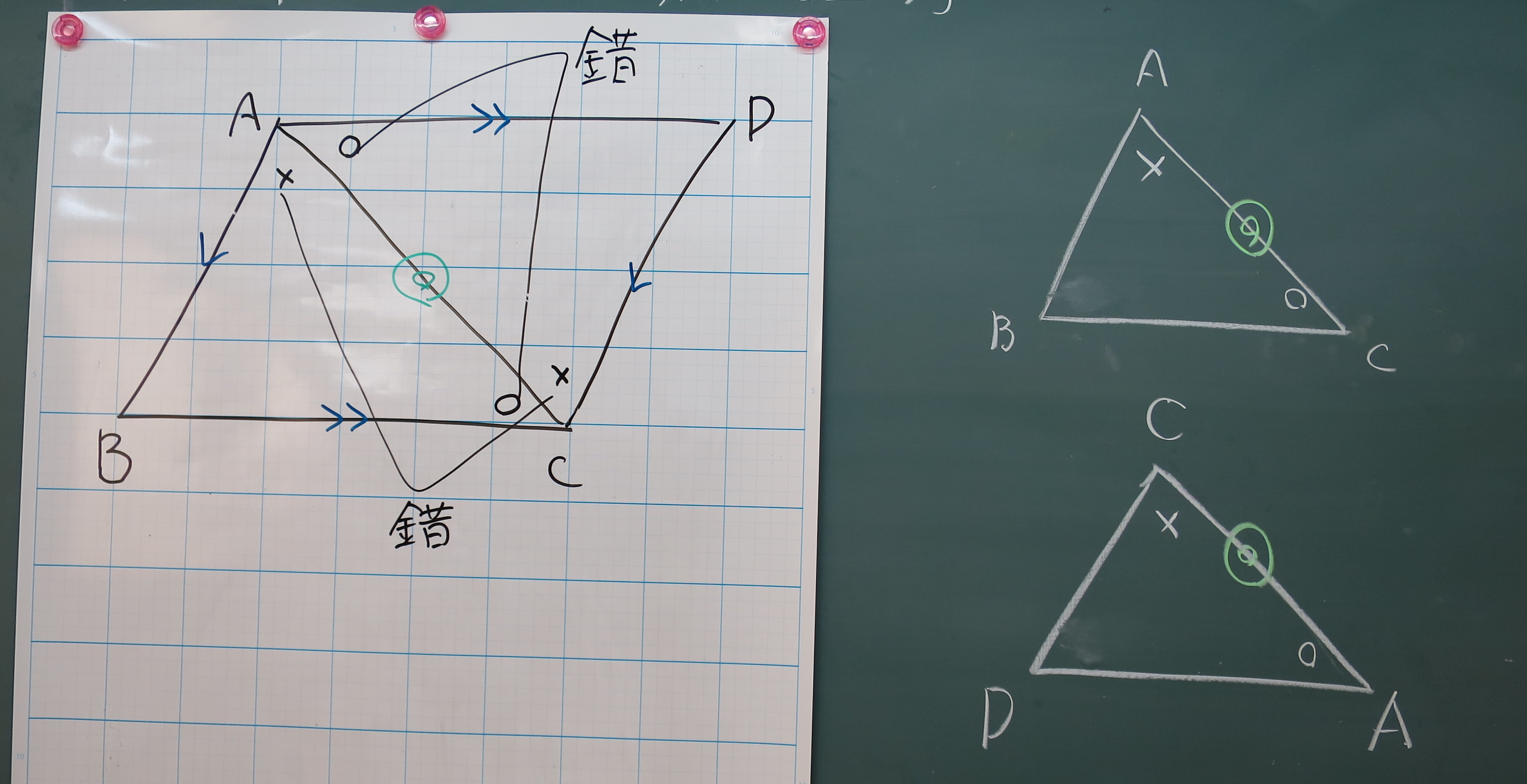



Tossランド 平行四辺形の性質
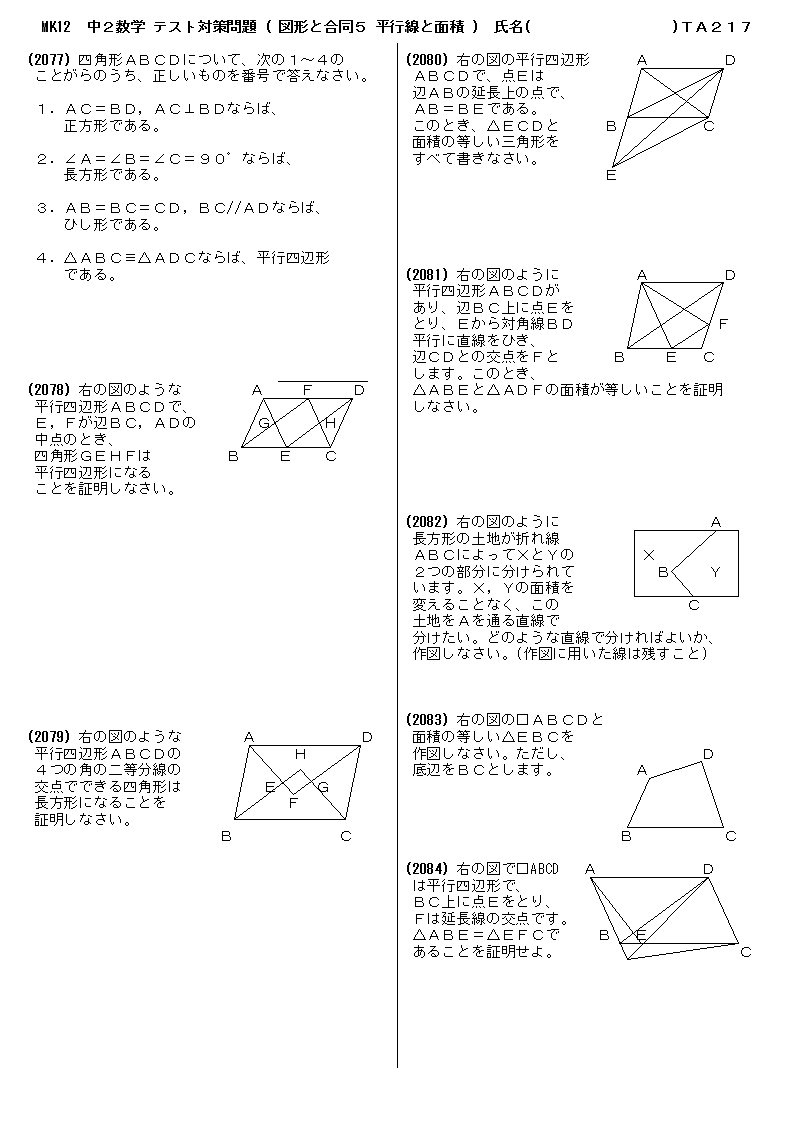



無料 中2数学 テスト対策 問題プリント 217 図形と合同5 平行線と面積
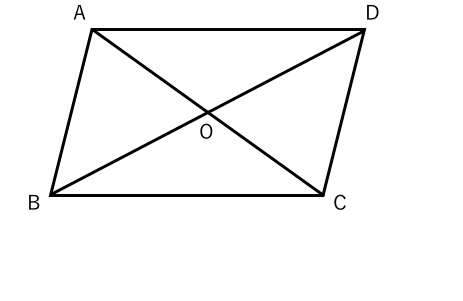



合同な三角形 平行四辺形で証明 苦手な数学を簡単に



1



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




平行四辺形と証明 Youtube




中2数学 三角形と四角形 章の問題a 赤城 ᐡᐤᐡ




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



中2 数学 5 3 平行四辺形の証明 Youtube



三角形と四角形 平行四辺形の辺や角の表記の順序 中学数学 定期テスト対策サイト



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生




平行四辺形の定義と性質 証明問題の解き方 数学fun




ม 2 โน ตของ 中2数学 平行四辺形の証明 授業ノート ช น Clear



1



1



平行四辺形の証明 2 ネット塾




平行四辺形abcdの頂点a Cから対角線bdに垂線を引き 対角線との交点をそれぞれ Clear
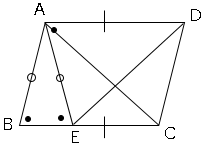



平行四辺形の合同の証明問題と角度を求める問題 数学の要点まとめ 練習問題一覧




中2 数学 中2 証明 中学生 数学のノート Clear
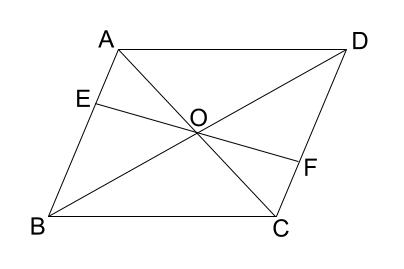



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
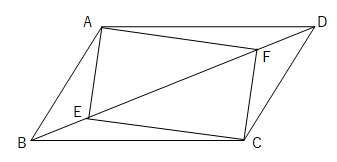



中2数学 平行四辺形の証明のポイントと練習問題 Examee




中2数学 合同証明 平行四辺形であることを証明 Youtube
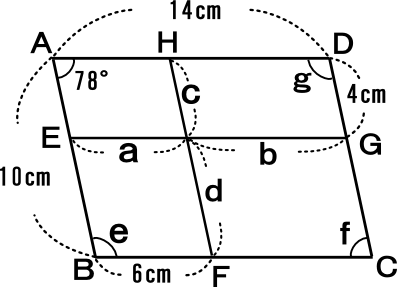



中学2年数学練習問題 図形と合同 平行四辺形の性質と証明問題



中学数学 中2合同の証明2 数樂管理人のブログ



特別な平行四辺形2



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
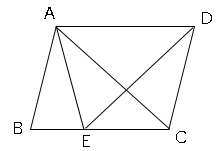



平行四辺形の合同の証明問題と角度を求める問題 数学の要点まとめ 練習問題一覧
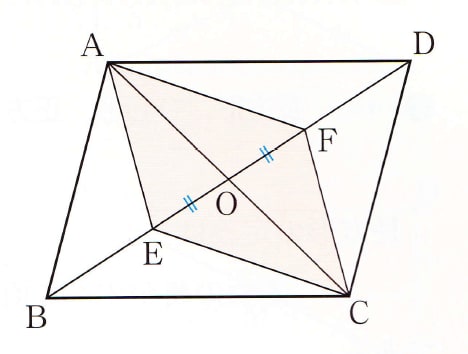



証明 は と が Takapの数学日記



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd



平行四辺形の性質1




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形



中2数学 平行四辺形の証明のポイントと練習問題 Examee




合同条件と性質について 中2 中3 家庭教師とっしゅ先生の授業 小学生 中学生


